1 Introduction
In many countries, a recent trend has been to include computational thinking (CT) in school curricula (Kafai and Proctor, 2022), either as a subject in its own right (e.g., England, Hungary, Greece, and Turkey), as part of an existing subject (e.g., Norway and France), or as a combination of the two (e.g., Finland) (Bocconi et al., 2022). This inclusion mirrors CT’s status as an essential 21st-century skill crucial for fostering children’s critical and analytical thinking (Voogt et al., 2015) and for promoting computer science-inspired abstract thinking, which is important for students’ future careers (Weintrop et al., 2016). Recently, in its revised school curriculum, Norway introduced CT into the mathematics, science, music, and arts and crafts curricula (Norwegian Directorate of Education and Training, 2020a). This imposed the need for mathematics teachers—whom we focus on in this article—to design classroom activities that include CT. While scholars such as Weintrop and Wilensky (2015) and Shute et al. (2017) have highlighted the natural ways in which CT and mathematics complement each other, many teachers have found the integration of CT into mathematics education challenging (Rich et al., 2019). This is often due to a lack of prior CT training, insufficient time for upskilling initiatives, and difficulties in finding connections between existing practices and CT (Reichert et al., 2020; Bocconi et al., 2022; Nordby et al., 2022b).
Recent efforts to define CT in school contexts have resulted in various ways of describing CT (Palts and Pedaste, 2020). For instance, in the literature on CT in education, researchers have inconsistently described CT as CT concepts (Barr and Stephenson, 2011), CT practices (Weintrop et al., 2016), CT perspectives (Brennan and Resnick, 2012), CT facets (Shute et al., 2017), CT aspects (Komm et al., 2020), and CT skills (Wing, 2006), resulting not only in confusion about what CT encompasses, but also about how to teach, learn, and assess CT (Kalelioglu et al., 2016; Tang et al., 2020). This lack of consensus makes it hard to find out what role CT shall play in the classroom (Israel and Lash, 2020; Lv et al., 2022; Nordby et al., 2022a). While there are researchers, such as Pérez (2018), who provide examples of what the relationship between CT and mathematical practices might look like, a gap between CT and mathematical practices within practical classroom activities is evident (Nordby et al., 2022a).
Despite the inconsistent ways of addressing CT in education, it is easy to get the impression that CT is often, if not always, included in mathematics classroom activities using different tools (see, e.g., Chan et al., 2023). Block-based programming languages (such as Scratch) and educational robotics (such as Bee-Bot) are often used in primary mathematics classroom (Nordby et al., 2022a). Therefore, in this paper, we focus on such tools which we refer to as CT tools. A major concern with most (if not all) of these CT tools is that, generally, activities that include their use most often produce CT activities rather than mathematical activities (Chan et al., 2023). Hence, more research is needed to investigate more closely how CT tools can be used in primary mathematics classroom activities in ways that enable a stronger focus on the learning of mathematics.
Considering the growth in the availability of CT tools (Chan et al., 2023), in this paper we report on two Norwegian primary school mathematics teachers’ attempts to integrate different CT tools into their teaching practices, while reflecting on how these CT tools can support the learning of mathematics. Hence, we propose the following research questions:
How and why are CT tools being integrated into primary mathematics classroom activities?
How do primary mathematics teachers, if at all, value the possible contributions of CT tools in teaching mathematics?
2 Literature review
Considering the vast number of CT tools available (Chan et al., 2023), and due to the focus of this paper, we continue here by reviewing the literature on how different visual block-based programming languages and educational robotics have been integrated and used in primary mathematics classroom activities. We have chosen not to include text-based programming languages as these are not common in primary mathematics classrooms.
2.1 Visual block-based programming languages
Several visual block-based programming languages have been developed for educational purposes, such as LogoBlocks, Alice, and Scratch (Weintrop and Wilensky, 2015). In visual block-based programming languages coding blocks are dragged and dropped to give instructions to solve the task at hand. Scratch is the most popular visual block-based programming language and is widely used to enhance students’ CT learning (Moreno-León and Robles, 2016).
While the literature shows that Scratch is mostly used in subject areas such as computer science and programming courses (Zhang and Nouri, 2019), there is also an increasing number of studies reporting on the use of Scratch in primary mathematics classrooms (see, e.g., Martinez et al., 2015; Calder, 2019). Studies on the use of Scratch in mathematics have focused on students’ mathematics learning (e.g., Rodríguez-Martínez et al., 2020; Laurent et al., 2022; Al-Otaibi et al., 2023) and mathematical thinking (Gadanidis et al., 2018; Miller, 2019), as well as on teachers’ reflections on using it in their mathematics classrooms (e.g., Sjöberg et al., 2018; Iyamuremye and Nsabayezu, 2022). In their systematic literature review, Nordby et al. (2022a) showed that only a few studies have reported on successful ‘full integrations’ where CT tools and mathematics showed to have a reciprocal relationship within primary mathematics classrooms’ activities. Nordby et al. (2022a) succeeded in finding only two such studies, namely that of Gadanidis et al. (2018), who used Scratch and Google’s Blocky to introduce students in Canada to the ideas of symmetry and group theory, and that of Miller (2019), who investigated Australian students’ mathematical thinking related to patterns and structures using Scratch. In addition, a more recent study of 21 primary teachers showed that teachers from Rwanda expressed positive views on using Scratch in their teaching of mathematics, as it ‘supports them to visualize abstract content’ (Iyamuremye and Nsabayezu, 2022, p. 1). While these studies provide examples of the potential of integrating CT tools in primary mathematics classroom activities, there are still few that have reported on activities where CT and mathematics have a reciprocal relationship.
A byproduct of Scratch, ScratchJr, is a programming environment aimed at children aged 5–7. In his systematic literature review, Stamatios (2022) showed that while most of the relevant studies (n = 18) reported ScratchJr to be helpful in teaching preschoolers about CT and basic coding skills, less is known about how it can play a role in the learning of mathematics. One study on the issue showed how ScratchJr was used in activities focusing on counting and pattern recognition for 4–7-year-old Latin American students (Vega et al., 2021). Pre-and post-test scores revealed that the use of ScratchJr had a positive effect ‘on the development of early mathematical skills in children from 4-to-5 years old’ (Vega et al., 2021, p. 253). As such, while Vega et al. (2021) showed that ScratchJr can provide advantages for the learning of mathematics, most studies do, however, report on ScratchJr being mainly used for coding activities (Stamatios, 2022).
2.2 Educational robotics
There have been research reports on different types of educational robotics used in primary mathematics classrooms, such as Lego Mindstorms and VBOT with physical robots (Ioannou and Makridou, 2018). In a systematic literature review, Seckel et al. (2023) investigated how 25 studies reported on the use of Bee-Bot (one educational robotic tool). Seckel et al. (2023) concluded that Bee-Bot was an appropriate resource for the development of CT skills, although little was said about the mathematical learning outcomes gained from using it. The missing out on mathematics learning opportunities seems to be a recurring concern; Bee-Bot is reported as being primarily used to learn CT. However, there have been some promising thoughts on how CT skills could be transferred to enhance mathematics learning (Angeli and Valanides, 2020; Cervera et al., 2020). For instance, Muñoz et al. (2020) reported on how Bee-Bot was used in developing logical mathematical thinking skills in Panama. They reported on students obtaining ‘a favorable level of performance in the different challenges proposed’ (Muñoz et al., 2020, p. 22).
A study by Bartolini Bussi and Baccaglini-Frank (2015) reports on how Bee-Bot was used in northern Italy to design primary mathematical classroom activities, focusing specifically on a mathematics learning goal. They reported on how Bee-Bot was used in primary mathematics classrooms to introduce the idea of rectangles for grade 1 students. By including activities using sequences of commands for creating rectangles, and from students’ notion of seeing it as a ‘squarized O’ (Bartolini Bussi and Baccaglini-Frank, 2015, p. 398), the authors concluded that Bee-Bot could contribute to students developing an understanding of what a rectangle is. Moreover, in a later study, Baccaglini-Frank et al. (2020) investigated Italian primary mathematics teachers’ ideas on using GeomBot educational robotics (similar to Bee-Bot) to create teaching activities that provide geometrical experiences for their students. Baccaglini-Frank et al. (2020) reported that GeomBot led teachers and students to focus on concepts such as internal and external angles. The teachers in the study agreed that working with GeomBot ‘provided greater ease’ (Baccaglini-Frank et al., 2020, p. 387) for the students to engage in mathematics. Baccaglini-Frank et al. (2020) suggested that GeomBot lead to new ways of discussing geometrical attributes in primary mathematics classrooms. The findings from these two studies (Bartolini Bussi and Baccaglini-Frank, 2015; Baccaglini-Frank et al., 2020) indicate that educational robotics has the potential to be used in a meaningful way in geometry.
There are also other variants of educational robotics used for promoting CT in education. One example is micro:bit, which is used in primary classrooms to promote students’ problem-solving skills and coding abilities (Carlborg et al., 2019; Brandhofer, 2021; Kalogiannakis et al., 2021). Studies where micro:bit is used in primary mathematics classrooms are sparse. Carlborg et al. (2019) used micro:bit to investigate how Swedish mathematics teachers produce teaching materials that can enhance students’ autonomy and scaffold their progression in basic programming concepts. As such, micro:bit was used to create activities where problem-solving, programming, and coding skills were foregrounded rather than mathematics. That being said, micro:bit also allows for connections to robotics, such as Bit:Bot (Lobnig et al., 2022). One small-scale intervention study conducted by Heim and Wang (2023) reported on how Bit:Bot can provide learning opportunities for Norwegian students within both programming and a specific subject, such as mathematics. While focusing on how 36 students perceived the possibilities of using programming in mathematics, Heim and Wang (2023) found that only seven reported that they found any connection between programming and mathematical contexts.
In sum, there is a growing body of research focusing on how CT tools promote CT skills in mathematics (e.g., Stamatios, 2022; Seckel et al., 2023). Relatively few studies have focused on how such tools can be used to facilitate primary mathematics classrooms activities. The studies that do exist show that there are opportunities for the use of CT tools to design such activities (see, e.g., Gadanidis et al., 2018; Baccaglini-Frank et al., 2020). More research is needed to understand not only how CT tools are being integrated into primary mathematics classroom activities, but also why. Furthermore, there is a need to understand whether primary mathematics teachers value the possible contribution of CT tools in teaching mathematics. Therefore, in this paper, we investigate the integration of CT tools in primary mathematics activities focusing not only on the ‘how’ but also on the ‘why’. Furthermore, inspired by the duration in the field reported on by Baccaglini-Frank et al. (2020) our paper reports over an eight-month data collection period.
3 Theoretical framework
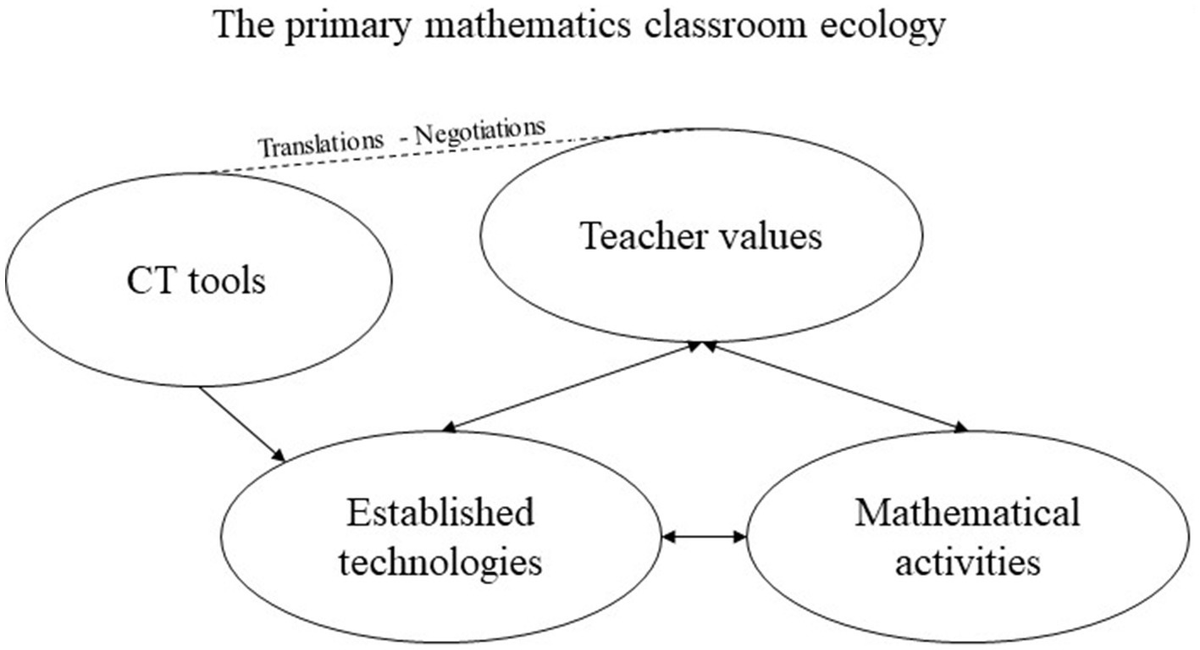
In this study, we draw on Nardi and O’Day’s (2000) notion of information ecology, understood as a ‘system of people, practices, values, and technologies in a particular local environment’ (Nardi and O’Day, 2000, p. 49). As such, the notion of information ecology can be used to investigate interactions between people and technologies within a specific ecology. When studying ecological systems, Nardi and O’Day (2000) highlight that evolution is important and often investigated in terms of how new technologies are established in already existing systems. New technologies enter ecological systems for a reason. For example, CT tools in the Norwegian mathematics classrooms was prescribed by the new curriculum (Norwegian Directorate of Education and Training, 2020a). In this study, we investigate how CT tools, as a new technology, are integrated into the primary mathematics classroom. While doing so, we view the primary mathematics classroom as a local ecological information system comprising people (teachers and students), practices (mathematical activities), values (teacher and student’s values), and technologies (tools used in mathematical activities).
When investigating the integration of different CT tools – as a new technology – into the primary mathematics classroom, we acknowledge, as suggested by Nardi and O’Day (2000), that these CT tools must be considered in the context of existing core values in the information ecology being studied. An example is the introduction of the calculator, where discussions of its place in the mathematics classroom ecology were grounded in whether activities facilitated by the calculator ‘fit’ with existing core values.
According to Nardi and O’Day (2000), it is the key actors in the ecology that determine and shape the new technology to fit into established practices. The key actors in this study are the primary mathematics teachers, as they are the ones that are responsible to ascribe meaning to using CT tools (as a new technology) within their existing teaching practice. Nardi and O’Day (2000) state that in determining how actors make sense of new technologies within an ecology, core values come into play. Within the primary mathematics classroom, core values typically focus on nurturing the best possible practices for mathematical learning, such as mathematical modeling (English, 2004).
Nardi and O’Day (2000) highlight that values are challenged by new technologies, possible entailing negotiation processes. These consist of interactions and interpretations that contribute to forming and defining the ecology. We suggest that integrating CT tools into primary mathematics teaching practices may lead to negotiation processes when teachers try to understand how CT tools can be used to design mathematical activities. Moreover, as stated by Nardi and O’Day (2000), the key actors may need to undertake some translating efforts in their negotiation process when attempting to adapt the use of the technology (here, CT tools) to fit into the established information ecology (the primary mathematics classroom). As such the integration of new technologies in established ecologies can also be a question of to which extent there is the need for translation, where little or no need for translation might lead to better chances of sustainability in the ecology (Nardi and O’Day, 2000).
Viewing CT tools as new technologies that have entered the primary mathematics classroom, a question that can be raised is how primary mathematics teachers value the possible contributions of CT tools in teaching mathematics. Drawing on and adapting Zhao and Frank’s (2003) model of a teaching eco-system, we place CT tools as the new technologies (see Figure 1). While Zhao and Frank (2003) focus on the broader eco-system, including the institutional school context, we zoom in on the primary mathematics classroom ecology, where we focus on how teachers may or may not need to negotiate or translate the activities that the CT tools facilitate in order to fulfill mathematical activities.
We continue by outlining our methodological choices that allow us to look at CT tools as ‘newcomers’ and to what extent they can be adopted in existing ecologies.
4 Methodology
Data were collected over a project period of 1.5 years where the focus was on investigating CT in primary mathematics education. In this paper we draw on data collected during the final 8 months of the project period. We focus on two teachers who, like most teachers in Norwegian primary schools, are non-specialists, meaning that they teach all subjects. They were recruited through convenience sampling, where the first author contacted various schools that signposted commitment to CT-related areas of focus on their schools’ web pages.
Since neither of the teachers had been trained in CT or programming, and both lacked previous experience in using different CT tools, this study was designed using a research-practice partnership approach (Coburn and Penuel, 2016). This approach enabled the first author to establish a long-term relationship with the two teachers to get an in-depth and comprehensive understanding of them integrating CT into their existing teaching practices. The first author actively participated in the planning and implementation of both teachers’ lessons, not as an expert, but by contributing with ideas and asking questions that prompted discussions and reflections. When one of the teachers for example planned an activity using the CT tool Bee-Bot, the first author could ask: ‘Where do you see the mathematics in this activity?’ or ‘How can we use this CT tool to create an activity with a mathematical focus?’. Also, when needed, the first author assisted both teachers conducting the lessons, helping out with practicalities.
The two teachers included in this study worked at different schools (both with approximately 600–700 students) in a large city in the eastern part of Norway. We proceed by giving a more detailed presentation of the two teachers (Olivia and Kimmi, both pseudonyms) and of how the participatory role of the first author played out. This is followed by a presentation of the study’s data collection methods, after which we end this section by outlining the steps taken in the analysis process.
4.1 Olivia
Olivia has 60 Credits in mathematics (equivalent to 1 year of full study) as part of her teacher education and 2 years of experience as a primary mathematics teacher. At the time of our study, Olivia was teaching grade 1 (aged 6–7 years), and 12 of her students agreed to participate (signed forms were provided by the students’ parents).
In agreement with the first author of this paper, Olivia decided to use an online license-based work package provided by the Norwegian Directorate of Education and Training (2020c). The aim of this work package was to help teachers integrate CT into existing subjects, such as mathematics. The work package included different modules directed to the subject of mathematics, and Olivia and the first author chose to use a module that provided plans and ideas suitable for grades 1–4. During the 8 months that the data collection took place, the following three modules were used: one on basic structures in programming, one on CT in mathematics, and one on programming in mathematics. The teaching plans and ideas in the work package were used for inspiration, while the actual activities were designed to fit the CT tools Olivia preferred to test and use, namely Codespark, Bee-Bot, ScratchJr, and an unplugged approach. Kamilla, one of Olivia’s colleagues, was invited to the planning sessions. Kamilla and Olivia were used to planning their mathematics lessons together, so instead of disrupting their routine, Kamilla participated with ideas and reflections on how CT tools could be used to design different mathematical classroom activities.
4.2 Kimmi
Kimmi has 30 ECTS in mathematics and 26 years of experience as a mathematics teacher. She was teaching mathematics in grade 5 (aged 10–11 years), and 24 of her students agreed to participate.
Kimmi did not use the license-based work package. Instead, through discussions with the first author regarding how to integrate CT into her teaching practice, Kimmi decided to involve a teacher responsible for technology at the school in one of the planning session of the CT-inspired lessons. This teacher introduced the educational robotics tool Bit:Bot to Kimmi. Consequently, Kimmi decided to use Bit:Bot in her first two lessons that were observed. In planning the next two lessons, Kimmi and the first author discussed how the block-based programming language Scratch could be integrated. Consequently, Scratch was the educational objective for the final two lessons.
4.3 Data collection
The data corpus consisted of planning sessions (audio-recorded), observations of lessons (video-recorded), and reflective conversations (audio-recorded). During the lessons that were observed, a wireless microphone was attached to the teacher, and a video camera was placed on a tripod. This enabled the first author to move the video camera around the classroom to capture the conversations the teachers had with their students. All the collected data were transcribed in full by the first author in the original language (Norwegian) and organized according to the CT tool that was used.
During the 8 months of data collection (see Figure 2), Olivia integrated four different CT tools—Codespark, Bee-Bot, ScratchJr, and an unplugged approach—into her teaching. The data collection from the Codespark and ScratchJr lessons consisted in total of four planning sessions (45–60 min), four lesson observations (35–40 min), and four reflective conversations (5–10 min). The Bee-Bot lessons consisted in total two planning sessions, three lessons observed and three reflective conversations. The unplugged approach consisted of one planning session, one observed lesson, and one reflective conversation.
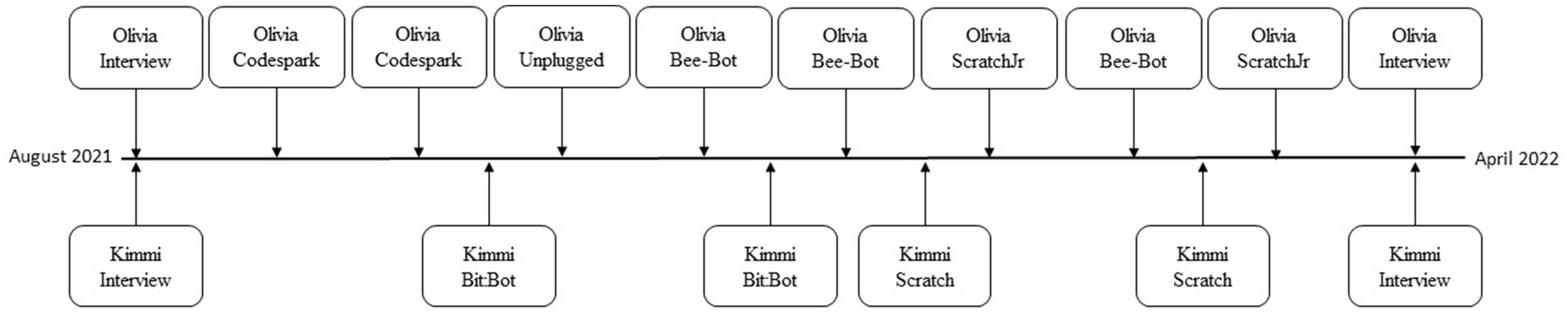
Figure 2. Data collection.
Kimmi used two different CT tools in her teaching, namely Bit:Bot and Scratch. The data collection from the Bit:Bot integration consisted of one planning session (45–60 min), two lesson observations (70–80 min), and one reflection conversation (5–10 min). The same amount of data was collected for the Scratch integration.
In addition to the sets of data described above, the first author conducted two semi-structured interviews with each teacher, one at the very beginning of this participatory project phase (30 min) (see the interview-guide in Appendix 1) and one at the end (60 min) (see the interview-guide in Appendix 2). The intention was to capture the two teachers’ reflections on the role that CT tools play in designing mathematics classroom activities before having tried them and after several conducted lessons. For instance, they were asked, ‘How do you think the different CT tools contribute to the mathematical activity?’ and ‘To what extent do you think that the CT tool can be integrated into the teaching of mathematics?’
The overall project was given ethical approval by the Norwegian Social Science Data Service, ensuring the interests of the participants. Written informed consent was obtained from the participating teachers and the parents of the participating students prior to the start of the research project.
4.4 Analysis
Drawing on Nardi and O’Day’s (2000) notion of information ecology, we used a deductive approach when analyzing our data in five steps using the Hyper Research software:
1. Transcription: The data, covering four interviews, nine planning sessions, 12 observation sessions and nine reflective conversations, were transcribed. Participants talk was transcribed. In addition, a description of activities during periods of silence, such as ‘students worked silently’, or ‘teachers read in their curricular materials’, in the observation data was included. Utterances that were not related to mathematics and/or CT (e.g., students discussions of what to do during the recess) were not transcribed. Non-verbal activities were transcribed when these were related to teaching and learning activities, but not transcribed if they were not related to mathematics and/or CT.
2. Identifying sequences: The data were content logged to identify sequences where both CT and mathematics were involved. In order to identify these sequences, we searched the data for specific activities or use of terms that involved the use of CT language such as ‘code [the Cat] it’ or ‘programming blocks’. We also searched the data for mathematics language such as ‘coordinates’ or ‘squares’. These excerpts were highlighted for further analysis. Sequences that did not involve both CT and mathematics were excluded as the focus in this paper is on the integration of CT in primary mathematics.
3. Categorization: The sequences where CT and mathematics were involved were categorized drawing on the information ecology perspective (Nardi and O’Day, 2000). An example of this is negotiation. In categorizing a sequence as ‘negotiation’, we studied how the teachers used the features in the CT tools (e.g., commanding blocks such as loops or steps) to facilitate mathematical content in the classroom, and whether the teacher needed to negotiate the use in order to meaningfully integrate the CT tool in their existing teaching practices.
4. Presentation: Data excerpts were selected for further analysis. Relevance was based on whether these were typical/atypical.
5. Translation into English: Excerpts selected for further analysis were translated into English after analysis in order to stay as close to the data as possible.
While the number of participants presented in this paper may initially seem limited, this limitation is offset by the researcher’s duration in the field. During the eight-month period that we spent in the field, and the combination of methods, planning sessions, observations and reflective conversation we were able to study the teachers’ practices in depth.
5 Results
The following section is organized according to the CT tools used by the teachers: Scratch, ScratchJr, Bee-Bot, and Bit:Bot–micro:bit. While focusing on how and why the CT tools were integrated into primary mathematics classroom activities and how the teachers valued them as part of their mathematics teaching practices, each section reports on the negotiations and translations needed.
5.1 Scratch
In one of the planning sessions, the first author and Kimmi discussed how Scratch, a CT tool Kimmi had previously used in her class, could be used to meet the mathematical goals outlined in the curriculum. Scratch is a programming environment that allow the students to combine different blocks to design for example games or stories (see Figure 3).
Figure 3. The programming environment in Scratch.
According to the Norwegian school curriculum for grade 6, students shall ‘use variables, loops, conditionals, and functions in programming to explore geometric shapes and patterns’ (Norwegian Directorate of Education and Training, 2020b). Consequently, in one of the planning sessions, Kimmi decided to use Scratch when designing activities for two of her lessons to ‘create geometric shapes, such as triangles, squares, circles, and spirals’ (Kimmi, planning session). In the following extract, Kimmi introduces Scratch to her grade 5 students and discusses how to create squares and rectangles:
1. Kimmi: When you click on this [Kimmi points to the green flag], you can start. It is also smart to have blocks from Control [the orange dot named ‘Control’] here is one called Repeat. Why is it smart to have Repeat?
2. Student: [Sound is unclear.]
3. Kimmi: Yes, it is true what you [the student] say, that you should repeat and do the same thing several times. But if you are creating a rectangle, can I repeat it four times, then?
4. Student: No.
5. Kimmi: No. Why not?
6. Student: Because all the sides are not the same length.
7. Kimmi: And what do we call it when all the sides are the same length?
8. Student: A square. But if we create a rectangle, then you can use Repeat twice.
In utterance 1, Kimmi introduces the program and the different ‘block’ commands to the students. She asks the students why ‘Repeat’ is a smart block to use when programming the Cat to move in a given number of steps (see Figure 4) making an effort of translating the language used in the CT tool into a mathematical context. In her introduction, Kimmi focuses on the CT concepts (Control and Repeat), and then turns the discussion to mathematics in utterance 3 by asking whether repeating the command ‘four times’ is the correct way of proceeding when creating a rectangle. The student’s response in utterance 6–8 reveals that he/she is fully aware of the difference between a square and a rectangle.
Figure 4. A reconstruction of Kimmi’s results after the whole-class conversation (the board image was unclear).
The Scratch environment accepts commands using the term ‘Steps.’ Both the teacher and the students easily accepted this as a translation of the mathematical term ‘length,’ which is needed when discussing geometric shapes (squares and rectangles) in terms of the length of their sides. In using terms that are readily accessible and that are easily translated into mathematical language, translation efforts are minimal between the CT tool and the discussion of the attributes of rectangles and squares. To a certain extent, the CT tool enables the visualization of mathematical activities, such as walking or drawing a geometrical shape. When the Cat ‘walks’ the shape, this gives room for discussing squares and rectangles in terms of geometrical attributes. The above discussion, while within the realm of mathematics, focuses on CT and understanding the role of commands such as ‘Repeat’. In the following, where the students and the teachers continue working with geometrical shapes, mathematics is foregrounded within the realm of the CT tool Scratch:
1. Kimmi: 150 [enters 150 steps into the block]. Okay!
2. Student: Then you need to turn 90 degrees.
3. Kimmi: Turn 90 degrees, okay. What do you want to do now? We moved 150 steps and turned 90 degrees.
4. Student: Walk 100 steps.
5. Kimmi: Why not 150?
6. Student: Because then it becomes a square.
In the above conversation, we see that mathematics is foregrounded. Kimmi does not mention what blocks the students should use, but rather how the selected blocks can be used to construct a rectangle. Utterance 4 and 5, for example, show how Kimmi and her students discuss what numbers to insert into the blocks for the shape to become a rectangle. The discussion in the above excerpt is therefore rooted in mathematics rather than in CT. As a CT tool, Scratch appeared to facilitate mathematical activities, fitting in with current practices.
However, despite the apparent ‘good fit’ between Scratch and mathematics, in the post interview, Kimmi pointed out a challenge, that can be seen as a negotiation with the CT tool, revealing doubts about its usefulness. She found its use to be connected only to ‘maybe mostly geometry’ (Kimmi, post-observation interview). Kimmi’s perspective was that this CT tool made a rather narrow contribution, as it was only usable in parts of her mathematics teaching practices.
5.2 ScratchJr
Olivia had some experience using ScratchJr when teaching Norwegian to her students and wanted to find ways to integrate it into her mathematics teaching as well. ScratchJr is a programable app, redesigned from Scratch, that allows the students to snap together blocks to make the Cat move (see Figure 5).
Figure 5. The ScratchJr environment with its turning blocks.
Olivia used ScratchJr in two of her grade 1 lessons to design activities involving squares and rectangles in the first lesson and coordinates in the second. During a planning session, Olivia recounted what she had planned for her lessons using ScratchJr, she wanted to ‘show them [the students] the grid, show them the starting block, and show them the blue ones [the motion blocks], and tell them to make the Cat walk in a quadrilateral.’ (Olivia, planning session). Olivia starts the lesson by introducing what blocks the student can use to create a quadrilateral in ScratchJr. At the end of the lesson, Olivia sums up the mathematics activity by choosing three students to present their work using a whiteboard projector. After having presented how one of the students solved the task of creating a quadrilateral, Olivia and the presenting student discussed the solution (see Figure 6):
1. Olivia: How many [programming blocks] are there straight ahead?
2. Student: Five.
3. Olivia: One, two, three, four, five [drawing the lines with a whiteboard marker depicting the movement blocks]. How many up?
4. Student: Three.
5. Olivia: Three. How many are there going back [referring to the blocks with arrows pointing left shown in Figure 6]?
6. Student: Five.
7. Olivia: And how many down?
8. Student: Three.
9. Olivia: Does the Cat walk in a square or a rectangle?
10. Student: Rectangle.
11. Olivia: Why’s that?
12. Student: Because there are two more; they are slightly longer than those [pointing at the lines].
13. Olivia: Yes, here, it takes five steps, and here, it takes three steps; here it takes five steps, and here it takes three. Do you agree that there are two short and two long sides?
14. Student: Yes!
15. Olivia: Yes. Then it is called a rectangle.
Figure 6. Image from the student’s explanation of how the Cat moves.
In the absence of a commanding block that visualized the movement of the Cat in ScratchJr, utterance 3 in the extract above and Figure 6 show how Olivia used a whiteboard marker to draw the identified steps. In utterance 1–8, the focus is on how many blocks the Cat has to ‘walk” to create a rectangle. Olivia asks the student in utterance 9 if the Cat walks in a square or a rectangle, which makes the student argue that the geometrical figure must be a rectangle, since the side lengths are unequal. Here, we see how Olivia uses the student’s solution in ScratchJr to discuss the characteristics of rectangles, by translating the program’s language to that of mathematics. Hence, the mathematical focus in the summing up appears to be twofold: first, counting the steps (as a means to measure length), and second, investigating geometrical shapes (a result of direction and counting).
Initially, it seemed that using ScratchJr did not require extensive translations to facilitate mathematical discussions of numbers (counting) and the relationship between numbers, directions, and the attributes of geometric shapes. However, during the lesson, we observed how some of the students ran into difficulties, as the figure drawn by the Cat took the form of a circle: ‘Mine [the Cat] only goes in a circle.’ (Student, observed lesson). Olivia’s workaround for this challenge was to use a whiteboard marker to draw the movement of the Cat ‘walking’ a rectangle. She highlighted that, as the interface in ScratchJr did not have a block command that could be used to draw the Cat’s movements, this challenged the visual representation of the rectangle:
I noticed that, because when they made small ones [squares], it was very difficult, and some said that it went in a circle. And I understand why they thought that, because it [the Cat] turns, so it can almost look like it is going in a circle … um … so I noticed when I drew the lines [on the whiteboard], and then they saw it. So, we should have had that pen (Olivia, reflective conversation)
As Olivia pointed out, it appears that the lack of a pen created the need for some translations while using the CT tool, where the aim was to understand the different attributes of geometrical shapes. Olivia’s workaround of using a whiteboard marker can be understood as a translation needed for the CT tool to facilitate what she found important in the activity. Using the CT tool was not enough to visualize the different attributes of geometrical shapes and could potentially lead to confusing images (a circle rather than a rectangle). The introduction of the whiteboard marker functioned to fill the gap between the teacher’s intentions for the mathematical activity and the limitations of the CT tool.
ScratchJr was also used by Olivia in the same class a few weeks later. The following extract shows how Olivia integrated ScratchJr to design a mathematical activity that focused on coordinates, as she found that coordinates was a part of its interface. Olivia introduced the lesson by uploading an image of a classroom and using it as a background scene in ScratchJr (see Figure 7). Olivia talked the students through their task by explaining how to code the Cat to move to a specific item in the ScratchJr background (from the bottom left to a drawer on the right in Figure 7) and to eventually find the new coordinates for the Cat.
1. Olivia: The first task is for you to place Scratch [Olivia used the name Scratch for the Cat] at the coordinates (3, 3). You can clearly see that there is a big blue circle around the coordinates—horizontal and vertical. Today, you must use only yellow and blue [movement] blocks. We always start with the yellow [block] and insert a starting block […] with a green flag. You can make [the Cat] go anywhere in the classroom. I think I want [the Cat] to walk to the drawers. Then, I must try to code him [the Cat] there. (..) [Olivia explains how she wants her blocks to be nine forward, six up, and six forward].
2. Olivia: So that will be my code. Let us see where he [the Cat] ends up (..). And then the question is, what coordinates is [the Cat] on now? He started in (3, 3). What are the coordinates now?
3. Student: (9, 18)
4. Olivia: (9, 18) (…) We always say the number that goes horizontally first, so the coordinates become (18, 9) [writes on the board using a whiteboard marker].
Figure 7. Olivia writes the coordinates from utterance 4 on the whiteboard.
Since Olivia had already used ScratchJr in a previous lesson, the students were familiar with how the CT tool worked. From the above extract, we can see that Olivia uses little time discussing the different blocks’ actions, but instead focuses on how they are used to move the Cat within the coordinate system. Utterance 1, for example, shows that Olivia only gave a brief explanation to her students about how to use the yellow and blue blocks (motion and event) before moving on to focus on mathematics in utterances 2–4. To direct the Cat to the desired location, Olivia uses CT language (‘code him’) as well as mathematical language (‘coordinates’) to show how both the CT tool and mathematics play an important role in the activity:
There is a grid and coordinate system and coordinates. Absolutely, that is what it is. … I feel that it was more the task [coordinates] now than only the coding. But you had to use your knowledge to create the codes to be able to get to those coordinates… so now the programming was used more to help to learn about coordinates (Olivia, reflective conversation).
As the extracts above illustrate, Olivia reflects on how she found ScratchJr to be suitable for promoting a mathematical activity involving coordinates. Olivia’s experience with ScratchJr when working with coordinates contrasts with her experience with the same tool when working with geometrical shapes. While ScratchJr entailed some translations on Olivia’s part, as the lack of pen or tracing led to mathematical misconceptions, (a square looked like a circle), there was little need for translations in working with coordinates.
5.3 Bee-bot
The educational robot Bee-Bot is a CT tool that Olivia’s school had bought. In this way, she found it interesting to use. To program and make the Bee-Bot move you push the buttons on top and push ‘go’ (a picture of the Bee-Bot is shown in Figure 8).
Figure 8. Top view of the Bee-Bot.
Olivia decided to design one activity where the Bee-Bot was used for a mathematical activity. The following extract shows how Olivia and Kamilla planned and discussed how and why they could integrate Bee-Bot to design a mathematical activity focusing on squares and rectangles:
1. Olivia: Yes, it [Bee-Bot] should return to where it starts, or should it then also go in a square?
2. Kamilla: Yes, because I think they [the students] can understand the term [square] just fine. Like, you can try [to create] the square, but you do not need to talk about the characteristics of the square but use the term. (..)
3. Olivia: Okay, I will draw it [the square] on the whiteboard so they can see what it is. But there is a difference between a square and a rectangle in the form of two, two, turn, two, two, turn, or if they take three, two, turn [referring to Bee-Bot’s movements]. This might be the first task, then.
In this conversation, Olivia and Kamilla agree that the CT tool can be used to teach the students about squares, but Olivia points out in utterance 3 that she wants to use Bee-Bot to point out the distinction between squares and rectangles to their students. Their conversation did not concern discussions about CT, but rather how this CT tool could be used to construct geometrical shapes in terms of the number of movements and turns. Initially, it appeared as if the teachers saw the potential for designing a mathematical activity involving squares and rectangles using the Bee-Bot.
Olivia started the lesson with a whole-class conversation about the difference between squares and rectangles on the whiteboard and how the Bee-Bot could be used to create movements of squares and rectangles. After a short introduction, Olivia made the students choose whether to work with a square or a rectangle and made them start by drawing the chosen shape on a piece of paper. Next, the students were told to draw the arrows needed to push on top of the Bee-Bot to make it move in their chosen shape (see Figure 9). When they finished drawing the arrows, they were asked to verify their ‘code’ by inserting it into the Bee-Bot and pushing GO. The following extract and Figure 9 show how one group of students, together with Olivia, worked on this task.
1. Olivia: Okay (…) How many steps must he [Bee-Bot] walk forward? What do you think?
2. Student: Three. [The student draws three forward arrows on the paper; see Figure 9.]
3. Olivia: Okay, now he [Bee-Bot] is standing here [pointing at the upper left corner of the rectangle on the sheet]. What is he going to do now?
4. Student: There. [Presses the left arrow on Bee-Bot and draws an arrow turning left.]
5. Olivia: Yes, turn around. Then he turned around and is now standing that way [moving Bee-Bot by lifting it and placing it in the correct direction]. What should he do now?
6. Student: Go down one. [The student draws one forward arrow on a new line on the paper.] (..)
7. Olivia: Okay, one down. So, what does he do? [The student pushes the left arrow on Bee-Bot and draws one right arrow.] Hmm, then he turns [lifting Bee-Bot]. How many steps does he have to walk now? [The student draws three forward arrows on the first line of the paper and inserts three forward arrows in Bee-Bot.]
8. Olivia: Yes, and then it comes here. [She points to the bottom right corner of the rectangle and lifts Bee-Bot to that place.] What must he do now? [The student pushes the left arrow but does not draw the arrow.] Yes, he must turn [Olivia turns Bee-Bot], and how many up? [The student pushes one up on Bee-Bot but does not draw the arrow.] Okay, let us try. [The student pushes GO, and Bee-Bot moves in a rectangle: three, turn left, one, turn left, three, turn left, and one.]
Figure 9. Students and Olivia working on creating a movement for Bee-Bot to walk the shape of a rectangle.
The extract shows how the Bee-Bot has the potential to promote a mathematical activity in two ways. First, the students were involved in a spatial experience involving squares. For example, utterance 5 shows how Olivia uses Bee-Bot as a physical representation to concretise correspondence between the arrows on top of Bee-Bot and how it moves on the floor. The combination of lifting the Bee-Bot to first indicate where it should move and later seeing the Bee-Bot’s own movements is an activity involving spatial insights into rectangles.
Second, the students were invited to focus on the length of the lines in creating a rectangle. By drawing the arrows before transferring the commands to Bee-Bot, (utterance 2) shows how the students were engaged in how many arrows and ‘pushes’ were needed to create, in this case, a rectangle. Both the spatial exploration and the use of the non-standard units of arrows show how the Bee-Bot has the ability to facilitate activities with squares and rectangles.
Adding of a sheet of paper used to draw the instructions that the students should insert into the Bee-Bot, reveals the translation efforts Olivia found necessary to concretise the actions of the Bee-Bot in the activity. Utterance 1 and 2, for example, show how Olivia encourages the student to demonstrate how many arrows, referred to as steps the students needed to program the Bee-Bot to move along the lines of the rectangle. However, this extract also shows how difficult it was for the students to write down the correct sequence. Utterance 8, for example, shows that the student does not draw one of the arrows, and Figure 9 shows that it is an error in the sequence of arrows, because the students lack accuracy in drawing the arrows in the right order. Consequently, it was not easy to understand which arrows on the sheet of paper corresponded to the buttons on Bee-Bot, and it was easy to make mistakes.
Both the need for translations and the challenges found here add to the question of whether the role and characteristics of Bee-Bot are good enough to correspond to the commonly accepted accounts of facilitating mathematical activities in primary mathematics classrooms. Olivia reflected upon these challenges in a reflective conversation:
It was like when I was sitting with those boys [one group of students], and then… I kind of kept trying to ask about […] why it went wrong—what happened that went wrong—and they struggled to answer … so then I kind of had to tell them that … now you started with him [Bee-Bot] looking the other way to where he was supposed to be looking, … but they, because they pressed [the buttons on Bee-Bot] so quickly and just pressed GO, then you can’t quite figure out where it went wrong. It might be a matter of practice for them, but it would obviously be easier if you could see the commanding blocks, as you can in Scratch (Olivia, post-observation interview).
Olivia evaluated the CT tool as having some characteristics that limited rather than encouraged mathematical activities, which she found easier with other CT tools, such as Scratch. The absence of a visualization also made Olivia reflect upon how easy it was to make mistakes, but also how difficult it was to uncover mistakes. These findings raise the question of whether translating efforts and the existing challenges contribute to negotiations against values, resulting in the CT tool not finding its rightful place within the primary mathematics classroom ecological system.
5.4 Bit:Bot–micro:Bit
Kimmi was introduced to the CT tool Bit:Bot by the teacher in charge of technology at the school. He provided her with instructions of how to use it. Kimmi chose to try the Bit:Bot in two of her grade 5 lessons. Bit:Bot, a robotic ‘car’ that is not a single tool but rather a collection of CT tools: a micro:bit, a programable chip, and a block-based programming environment connected to the micro:bit (see Figure 10). The Bit:Bot is controlled by the micro:bit.
Figure 10. (A) The Bit:Bot with the attached MicroBit, showing the marker holder and its marker. (B) The block-based programming environment needed for programming the MircoBit.
Kimmi’s main goal in designing a classroom activity was to get ‘[the students] to try to make it [Bit:Bot] move and then come back’ (Kimmi, planning session). While explaining these blocks to her students, Kimmi discussed how they could get Bit:Bot to move:
When you press driving, there are many kinds of commands. (…) Drive forward at a speed of 60%. It’s a bit difficult to know what 60% is, so we must try our best. (…) Drive forward at a speed of 60% for 400 milliseconds. Just how far? How much like that … these numbers here … you must adjust … and know … and understand … so you must try. I used this with a speed of 60%, then I turned with less speed there [pointing at the fourth block], and I had to repeat it four times. I also had this [pointing at the fifth block] repeat four times. And if we intend to return to the starting point, we must just try.
As we can see from the above extract and Figure 11, a prerequisite in Bit:Bot is the use of mathematical language. When Kimmi wanted Bit:Bot to move to the right, she used the block ‘drive right with speed 60% for 400 milliseconds.’ However, it was clear that this mathematical language was unfamiliar to the teacher: ‘It is difficult… we must try our best.’ Kimmi did not quite understand how the mathematics in the blocks connected to Bit:Bot’s movements, revealed by how she repeatedly said, ‘You must just try.’ Substantial translations in mathematical language were therefore needed to understand what driving at a speed of 60% for 400 milliseconds actually meant in practice. However, these translations were difficult for the teacher to understand and use, resulting in both the teacher and the students to use trial and error.
Figure 11. Kimmi’s example of her sequence of block commands.
In the post-observation interview, Kimmi highlighted how she struggled to understand how this CT tool could be an active feature in her teaching activities when she was asked how it contributed to mathematics:
No, I still find it difficult. Like the micro:bit, for example, so I sort of did not see a connection at all. […] You maybe must set a degree and sort of think about […] the milliseconds and things like that, and you use numbers. But […] it might as well be science, because it contributes to exploration. So, you could call the subject technology (Kimmi, post-observation interview).
Kimmi is clearly unsure of how this CT tool can contribute to her mathematics teaching practice. She found it difficult to ‘build a bridge’ between the mathematical language used in the CT tool and the mathematical language used in her primary mathematics classroom. As such, on the basis of Kimmi’s negotiations against what she valued as important for her teaching practice, she found that Bit:Bot was not suitable for mathematical activities in grade 5, but instead she saw it as a CT tool that could be used in other subjects, such as science or technology. This raises the issue of whether this CT tool is too complex for mathematical classrooms at this level. Consequently, it may be too much work for teachers to bridge activities with the CT tool to existing activities in a primary mathematics classroom ecological system. It is therefore not clear what purpose and added contribution Bit:Bot has in such a system.
5 Discussion
By drawing on an information ecology perspective (Nardi and O’Day, 2000), we discuss how and why CT tools can be integrated into primary mathematics classroom activities and whether or not teachers value the CT tools’ possible contributions.
We recognize that the integration of a CT tool into a mathematics classroom ecological system can stage negotiations with the primary mathematics teachers’ values, which, in terms of Nardi and O’Day’s (2000) arguments, will affect their choices regarding what can and cannot be done. Hence, we start by discussing how attempts were made to integrate the four CT tools presented in the Results section into the two teachers’ mathematics teaching practices. We do this by bringing to the fore two instances of translations that did not call for any negotiations and one that did. This eventually leads us to raise some issues in relation to how and why CT tools are integrated and found to be suitable for primary mathematics activities. We end this discussion by drawing attention to how the two teachers valued the CT tools’ possible contributions.
First, from an information ecology perspective, both Scratch and ScratchJr appeared to use a language that was readily accessible and that made the translation between the given CT language and the mathematics language redundant. The ‘steps’ in both Scratch and ScratchJr can be linked to non-standardized measures for length. This was rather different from Bit:Bot, where Kimmi struggled to find how the language used could be mathematically relevant for her grade 5 students, a finding that adds to those of Heim and Wang (2023), who found a limited connection between Bit:Bot’s features and primary mathematics. From an information ecology perspective, this limited connection appears to be partly due to the language used in the CT tool. This counterexample partly strengthens the finding of the role of language in the CT tool. For CT tools such as Scratch and ScratchJr, where translation efforts were minimal between the CT tool and the discussion of the attributes of rectangles and squares. This appeared to facilitate the meaningful integration of the CT tool into the teacher’s primary mathematics activities—non-standard units of measurement are prominent in the Norwegian curriculum for mathematics in grade 2. As such, while Gadanidis et al. (2018) and Iyamuremye and Nsabayezu (2022) showed how teachers were positive about using Scratch, this study expands on their findings by showing examples of why the teachers were positive.
Second, when talking about Scratch, ScratchJr, and Bee-Bot, there was no need for the teachers to negotiate a ‘place’ for integrating the CT tool in their mathematics teaching, as the teachers found these CT tools to be conducive in foregrounding mathematics discussions. These findings are in line with those reported in other research studies, for example, that Scratch is found useful in the learning of symmetries (Gadanidis et al., 2018), ScratchJr in the introduction of counting and pattern recognition (Vega et al., 2021), and Bee-Bot when exploring squares (Bartolini Bussi and Baccaglini-Frank, 2015), to name a few. Furthermore, we also saw traces of more advanced mathematics in using ScratchJr for introducing coordinates to grade 1 students. This is in line with Gadanidis et al.’s (2018) findings where Scratch was used to introduce students in grades 3 and 6 to symmetry and group theory, the latter being a very advanced topic for primary students. Based on these findings, it appeared that Scratch, ScratchJr, and Bee-Bot contributed opportunities for primary mathematics activities, but we also found an instance where more translations was needed.
When using both ScratchJr and Bee-Bot, Olivia used different methods of translations that staged negotiations; however, in two different ways. First, when challenged by how the Cat in ScratchJr did not leave a trace, Olivia decided to use a pen to draw the Cat’s route. While the use of the pen can be viewed as a way of translations needed for meeting the immediate challenge of the Cat depicting an ‘invisible’ shape, which was necessary because the Cat’s behavior disrupted the teacher’s practice of making mathematics visible to her students. Such disruptions will, according to Nardi and O’Day (2000), contribute to the human actor’s values which in turn affect their experiences of the possibility of using such technologies. The disruption here contributed to an evaluation that a pen was needed to better visualize the results of the Cat’s walk. This observation makes it legitimate to ask whether this CT tool inhibits more than it promotes mathematical activities and, as such, raises issues of whether these tools have a place in the primary mathematics classroom ecological system.
Second, in line with Bartolini Bussi and Baccaglini-Frank (2015), our analysis showed that Bee-Bot can contribute meaningfully to mathematics classroom activities that focus on understanding rectangles. However, as with the Cat in ScratchJr, Bee-Bot does not leave a trace. This time, Olivia solved this issue by including a piece of paper on which the students were told to draw arrows that, in turn, visualized Bee-Bot’s movements on the floor. This action of visualizing the process can be regarded as what Nardi and O’Day (2000) talk about as a translation. The sheet of paper contributes to visualizing both instructions and the shape of the geometrical figure. These translations were staged in order for the CT tool to fit better with what the teachers considered to be mathematically relevant within primary mathematics education.
Finally, we draw attention to how the two teachers valued the CT tools’ possible contributions, acknowledging that the actors in a local ecological system value new technologies according to their utility (Nardi and O’Day, 2000). Our findings indicate that there is compliance between how the teachers value the CT tools’ possible contributions and the discussion above on the need for translations. A significant point is that how and why translations are staged, appear to influence the extent to which teachers find the CT tool meaningful or not. For example, even if ScratchJr appeared to use a language that was readily accessible, and therefore needed no translation in that regard, translations were needed at other times because the teacher was challenged by what the CT tools could accomplish, in this case by how the Cat in ScratchJr did not leave a trace in drawing geometrical shapes. Such a need for translation lowered the CT tool’s contribution, because it spurred negotiations against what the teacher finds important in the primary mathematics teaching practice.
Of the four CT tools included in our analysis, Scratch was the only CT tool where the teacher did not need to use extensive translations to make the activity fit into the teaching practices. However, despite this apparent ‘good fit’, the teacher had retrospective doubts about its usefulness. The teacher found that Scratch was suitable only for geometry learning. The focus on geometry learning when integrating Scratch as a CT tool is also prominent in the research literature, where studies have focused on using Scratch for geometry learning, such as patterns (Miller, 2019) and symmetry (Gadanidis et al., 2018). However, and issue can be raised if there is any point in using a substantial amount of time for both teachers and students to integrate a CT tool if it can only be used in limited parts of a mathematical topic? Will these efforts be worth it in terms of what opportunities for learning the CT tool can provide? These issues warrant further investigations.
In line with previous studies, our findings also highlight the need for upskilling initiatives for mathematics teachers (Sands et al., 2018; Reichert et al., 2020; Bocconi et al., 2022). Primary mathematics teachers need to learn more about how and when to include what CT tool. That is, we find, in line with Weintrop et al. (2016), that teachers need to learn to choose the appropriate CT tool for a given task. In sum, understanding not only how but also why teachers integrate and use CT tools in their teaching of mathematics, contributes to a better understanding of teachers’ value of CT tools in the teaching of mathematics, and additionally, of the role that CT play in teaching mathematics. We assert that a better understanding of the role of CT tools in primary mathematics classroom ecologies has implications for both future developments of CT tools, and also for the requested upskilling initiatives. However, more research is needed to further explore which CT tools are beneficial for designing primary mathematical activities. Currently, it appears that integrating CT tools into primary mathematics teaching practices is a challenging task for teachers. Considering the varied approaches to integrating CT into education globally, further research is needed to determine whether CT tools should continue to be taught as a standalone subject, within other subjects, or as a combination of the two.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author/s.
Ethics statement
The studies involving humans were approved by SIKT, with the contact person Bellinda Gloppen Helle. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin. Written informed consent was obtained from the individual(s), and minor(s)’ legal guardian/next of kin, for the publication of any potentially identifiable images or data included in this article.
Author contributions
SN: Writing – original draft, Writing – review & editing. LM: Supervision, Writing – review & editing, Conceptualization, Formal analysis, Validation. AB: Supervision, Writing – review & editing, Formal analysis, Methodology, Validation.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This project was funded by the Research Council of Norway (Grant no. 320322).
Acknowledgments
We wish to thank the participating teachers for their contributions and discussions, which made this study possible. We also wish to thank the reviewers for their constructive feedback, which contributed to the improvement of this study.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at:
References
Al-Otaibi, M. M., Al-Otaibi, H. M., and Farghal, T. M. A. (2023). The effect of teaching mathematics using scratch software on the achievement of 6th grade students in Kuwait. Migr. Lett. 20, 288–304. doi: 10.59670/ml.v20iS1.3581
Crossref Full Text | Google Scholar
Angeli, C., and Valanides, N. (2020). Developing young children’s computational thinking with educational robotics: an interaction effect between gender and scaffolding strategy. Comput. Hum. Behav. 105:105954. doi: 10.1016/j.chb.2019.03.018
Crossref Full Text | Google Scholar
Baccaglini-Frank, A. E., Santi, G., Del Zozzo, A., and Frank, E. (2020). Teachers’ perspectives on the intertwining of tangible and digital modes of activity with a drawing robot for geometry. Educ. Sci. 10:387. doi: 10.3390/educsci10120387
Crossref Full Text | Google Scholar
Barr, V., and Stephenson, C. (2011). Bringing computational thinking to K-12: what is involved and what is the role of the computer science education community? Acm Inroads 2, 48–54. doi: 10.1145/1929887.1929905
Crossref Full Text | Google Scholar
Bartolini Bussi, M. G., and Baccaglini-Frank, A. (2015). Geometry in early years: sowing seeds for a mathematical definition of squares and rectangles. ZDM 47, 391–405. doi: 10.1007/s11858-014-0636-5
Crossref Full Text | Google Scholar
Bocconi, S., Chioccariello, A., Kampylis, P., Dagienė, V., Wastiau, P., Engelhardt, K., et al. (2022). Reviewing computational thinking in compulsory education.
Google Scholar
Brandhofer, G. (2021). The micro:bit and computational thinking: evaluation results of a computational project. Mobile learning and educational technologies. International Association for Development of the Information Society, pp. 57–64.
Google Scholar
Brennan, K., and Resnick, M. (2012). New frameworks for studying and assessing the development of computational thinking. Proceedings of the 2012 annual meeting of the American Educational Research Association, Vancouver, Canada.
Google Scholar
Calder, N. (2019). Using scratch to facilitate mathematical thinking. Waikato J. Educ. 23, 43–58. doi: 10.15663/wje.v23i2.654
Crossref Full Text | Google Scholar
Carlborg, N., Tyrén, M., Heath, C., and Eriksson, E. (2019). The scope of autonomy when teaching computational thinking in primary school. Int. J. Child Comput. Interact. 21, 130–139. doi: 10.1016/j.ijcci.2019.06.005
Crossref Full Text | Google Scholar
Cervera, N., Diago, P. D., Orcos, L., and Yáñez, D. F. (2020). The acquisition of computational thinking through mentoring: an exploratory study. Educ. Sci. 10:202. doi: 10.3390/educsci10080202
Crossref Full Text | Google Scholar
Chan, S.-W., Looi, C.-K., Ho, W. K., and Kim, M. S. (2023). Tools and approaches for integrating computational thinking and mathematics: a scoping review of current empirical studies. J. Educ. Comput. Res. 60, 2036–2080. doi: 10.1177/07356331221098793
Crossref Full Text | Google Scholar
Coburn, C. E., and Penuel, W. R. (2016). Research–practice partnerships in education: Outcomes, dynamics, and open questions. Educ. Res. 45, 48–54. doi: 10.3102/0013189X16631750
Crossref Full Text | Google Scholar
English, L. (2004). Mathematical modelling in the primary school. Proceedings of the 27th annual conference of the mathematics education research Group of Australasia: Mathematics education for the third millennium: Towards 2010 (Vol. 1 pp. 207–214).
Google Scholar
Gadanidis, G., Clements, E., and Yiu, C. (2018). Group theory, computational thinking, and young mathematicians. Math. Think. Learn. 20, 32–53. doi: 10.1080/10986065.2018.1403542
Crossref Full Text | Google Scholar
Heim, G., and Wang, O. J. (2023). Block and unplugged programming can be mutually beneficial: a study of learning activities in a 6th grade class in Norway. Front. Education. 8:1138285. doi: 10.3389/feduc.2023.1138285
Crossref Full Text | Google Scholar
Ioannou, A., and Makridou, E. (2018). Exploring the potentials of educational robotics in the development of computational thinking: a summary of current research and practical proposal for future work. Educ. Inf. Technol. 23, 2531–2544. doi: 10.1007/s10639-018-9729-z
Crossref Full Text | Google Scholar
Israel, M., and Lash, T. (2020). From classroom lessons to exploratory learning progressions: mathematics + computational thinking. Interact. Learn. Environ. 28, 362–382. doi: 10.1080/10494820.2019.1674879
Crossref Full Text | Google Scholar
Iyamuremye, A., and Nsabayezu, E. (2022). Mathematics and science teachers’ conception and reflection on computer programming with scratch: technological and pedagogical standpoint. Int. J. Educ. Train. Learn. 6, 11–16. doi: 10.33094/ijetl.v6i1.488
Crossref Full Text | Google Scholar
Kafai, Y. B., and Proctor, C. (2022). A revaluation of computational thinking in K–12 education: moving toward computational literacies. Educ. Res. 51, 146–151. doi: 10.3102/0013189X211057904
Crossref Full Text | Google Scholar
Kalelioglu, F., Gulbahar, Y., and Kukul, V. (2016). A framework for computational thinking based on a systematic research review. Baltic J. Mod. Comput. 4, 583–596.
Google Scholar
Kalogiannakis, M., Tzagaraki, E., and Papadakis, S. (2021). A systematic review of the use of BBC micro: bit in primary school. In conference Proceedings New Perspectives in Science Education 2021.
Google Scholar
Komm, D., Hauser, U., Matter, B., Staub, J., and Trachsler, N. (2020). Computational thinking in small packages. In informatics in schools. Engaging learners in computational thinking: 13th international conference, ISSEP 2020, Tallinn, Estonia, November 16–18, 2020, proceedings 13. Berlin: Springer International Publishing, 170–181.
Google Scholar
Laurent, M., Crisci, R., Bressoux, P., Chaachoua, H., Nurra, C., de Vries, E., et al. (2022). Impact of programming on primary mathematics learning. Learn. Instr. 82:101667. doi: 10.1016/j.learninstruc.2022.101667
Crossref Full Text | Google Scholar
Lobnig, N., Wieser, M., Pasterk, S., and Bollin, A. (2022). Teaching fundamental programming concepts with the BBC micro:Bit. Vienna, Austria, Sep. 25th–Sep. 28th, 2022, 67.
Google Scholar
Lv, L., Zhong, B., and Liu, X. (2022). A literature review on the empirical studies of the integration of mathematics and computational thinking. Educ. Inf. Technol. 28, 8171–8193. doi: 10.1007/s10639-022-11518-2
Crossref Full Text | Google Scholar
Martinez, C., Gomez, M. J., and Benotti, L. (2015). A comparison of preschool and elementary school children learning computer science concepts through a multilanguage robot programming platform. In proceedings of the 2015 ACM conference on innovation and technology in computer science education, pp. 159–164.
Google Scholar
Miller, J. (2019). STEM education in the primary years to support mathematical thinking: using coding to identify mathematical structures and patterns. ZDM 51, 915–927. doi: 10.1007/s11858-019-01096-y
Crossref Full Text | Google Scholar
Moreno-León, J., and Robles, G. (2016). Code to learn with scratch? A systematic literature review. In: 2016 IEEE global engineering education conference (EDUCON), pp. 150–156.
Google Scholar
Muñoz, L., Villarreal, V., Morales, I., Gonzalez, J., and Nielsen, M. (2020). Developing an interactive environment through the teaching of mathematics with small robots. Sensors 20:1935. doi: 10.3390/s20071935
PubMed Abstract | Crossref Full Text | Google Scholar
Nardi, B. A., and O’Day, V. (2000). Information ecologies: Using technology with heart. Cambridge, MA: MIT Press.
Nordby, S. K., Bjerke, A. H., and Mifsud, L. (2022a). Computational thinking in the primary mathematics classroom: A systematic review. Digit. Exp. Math. Educ. 8, 27–49. doi: 10.1007/s40751-022-00102-5
Crossref Full Text | Google Scholar
Nordby, S. K., Bjerke, A. H., and Mifsud, L. (2022b). Primary mathematics teachers’ understanding of computational thinking. KI-Kunstl. Intell. 36, 35–46. doi: 10.1007/s13218-021-00750-6
Crossref Full Text | Google Scholar
Google Scholar
Palts, T., and Pedaste, M. (2020). A model for developing computational thinking skills. Inf. Educ. 19, 113–128. doi: 10.15388/infedu.2020.06
Crossref Full Text | Google Scholar
Pérez, A. (2018). A framework for computational thinking dispositions in mathematics education. J. Res. Math. Educ. 49, 424–461. doi: 10.5951/jresematheduc.49.4.0424
Crossref Full Text | Google Scholar
Reichert, J. T., Barone, D. A. C., and Kist, M. (2020). Computational thinking in K-12: an analysis with mathematics teachers. EURASIA J. Math. Sci. Technol. Educ. 16:7832. doi: 10.29333/ejmste/7832
Crossref Full Text | Google Scholar
Rich, K. M., Yadav, A., and Schwarz, C. V. (2019). Computational thinking, mathematics, and science: elementary teachers’ perspectives on integration. J. Technol. Teach. Educ. 27, 165–205.
Google Scholar
Rodríguez-Martínez, J. A., González-Calero, J. A., and Sáez-López, J. M. (2020). Computational thinking and mathematics using scratch: an experiment with sixth-grade students. Interact. Learn. Environ. 28, 316–327. doi: 10.1080/10494820.2019.1612448
Crossref Full Text | Google Scholar
Sands, P., Yadav, A., and Good, J. (2018). “Computational thinking in K-12: in-service teacher perceptions of computational thinking” in Computational thinking in the STEM disciplines. ed. M. S. Khine (Berlin: Springer), 151–164.
Google Scholar
Seckel, M. J., Salinas, C., Font, V., and Sala-Sebastià, G. (2023). Guidelines to develop computational thinking using the bee-bot robot from the literature. Educ. Inf. Technol. 28, 16127–16151. doi: 10.1007/s10639-023-11843-0
Crossref Full Text | Google Scholar
Shute, V. J., Sun, C., and Asbell-Clarke, J. (2017). Demystifying computational thinking. Educ. Res. Rev. 22, 142–158. doi: 10.1016/j.edurev.2017.09.003
Crossref Full Text | Google Scholar
Sjöberg, C., Nouri, J., Sjöberg, R., Norén, E., and Zhang, L. (2018). Teaching and learning mathematics in primary school through scratch. EDULEARN18 proceedings, pp. 5625–5632.
Google Scholar
Stamatios, P. (2022). Can preschoolers learn computational thinking and coding skills with ScratchJr? A systematic literature review. Int. J. Educ. Reform 33, 28–61. doi: 10.1177/10567879221076077
Crossref Full Text | Google Scholar
Tang, X., Yin, Y., Lin, Q., Hadad, R., and Zhai, X. (2020). Assessing computational thinking: A systematic review of empirical studies. Comput. Educ. 148:103798. doi: 10.1016/j.compedu.2019.103798
Crossref Full Text | Google Scholar
Vega, B., Velasco, M., Ocaña, M., and Rebeca, M. (2021). “Scratchjr visual programming language for early math skills development in 4–7 years old children” in Emerging Research in Intelligent Systems. eds. M. Botto-Tobar, H. Cruz, A. D. Cadena, and B. Durakovic (Berlin: Springer), 245–258.
Google Scholar
Voogt, J., Fisser, P., Good, J., Mishra, P., and Yadav, A. (2015). Computational thinking in compulsory education: towards an agenda for research and practice. Educ. Inf. Technol. 20, 715–728. doi: 10.1007/s10639-015-9412-6
Crossref Full Text | Google Scholar
Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L., et al. (2016). Defining computational thinking for mathematics and science classrooms. J. Sci. Educ. Technol. 25, 127–147. doi: 10.1007/s10956-015-9581-5
Crossref Full Text | Google Scholar
Weintrop, D., and Wilensky, U. (2015). To block or not to block, that is the question: Students’ perceptions of blocks-based programming. In: proceedings of the 14th international conference on interaction design and children. Association for Computing Machinery, pp. 119–208.
Google Scholar
Zhang, L., and Nouri, J. (2019). A systematic review of learning computational thinking through scratch in K-9. Comput. Educ. 141:103607. doi: 10.1016/j.compedu.2019.103607
Crossref Full Text | Google Scholar
Zhao, Y., and Frank, K. A. (2003). Factors affecting technology uses in schools: An ecological perspective. Am. Educ. Res. J. 40, 807–840. doi: 10.3102/00028312040004807
Crossref Full Text | Google Scholar
link